(Python) 백준 온라인저지 - 가치있는 시간

쉬운 목차

문제

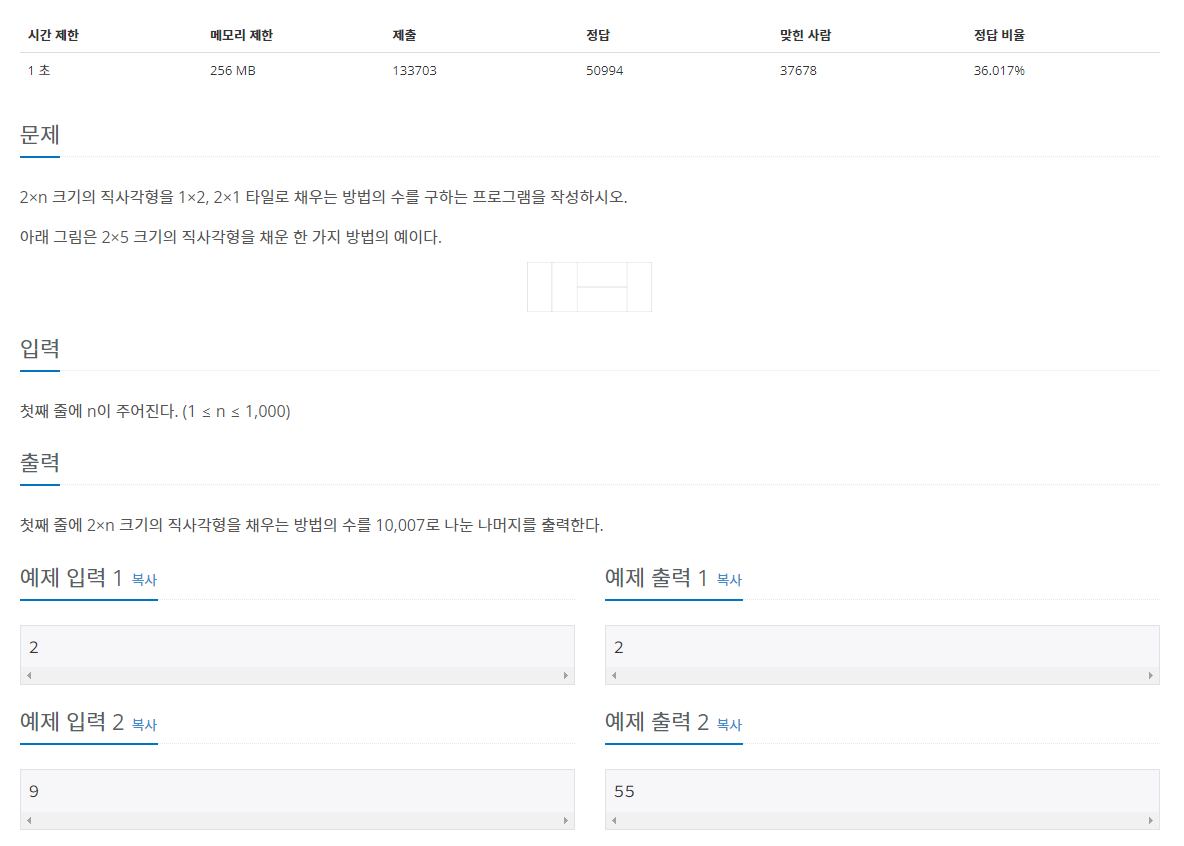
솔루션 프로세스

고등학교 수학 시간에 만났던 문제가 기억나는데 발화 공식이 모호합니다.

경우의 수를 풀고 나면 아…!
나는 기억했다.
요약하면 반복 방정식은 피보나치 수열과 동일합니다.

'추천 관련글,

피보나치 수열이란 무엇입니까?
1, 1, 2, 3, 5, 8, 13, 21, …과 같은 수열. 여기서 다음 항은 이전 항의 합입니다.

(항은 다음과 같이 계속됩니다: 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5…. 물론 처음 두 항을 정의해야 합니다.
)
따라서 재귀 공식은 다음과 같습니다.

F(n+2) = F(n+1) + F(n) (F(0) =1, F(1) = 1)

피보나치 수열이 정답이라는 것을 깨닫기 전에, 나는 스스로 경우의 수를 세어 보았다.

2 x 5의 크기에 도달해야만 경우의 수를 고려하고 ‘피보나치 수열인가?’ 의심이 들었지만 2 x 6 크기가 나를 이겼습니다.

다른 분들의 블로그 솔루션을 보고 왜 정답이 피보나치 수열인지 이해할 수 있었습니다.

먼저 2 x (n – 1)에서 2 xn으로 확장할 수 있는 경우를 살펴보겠습니다.

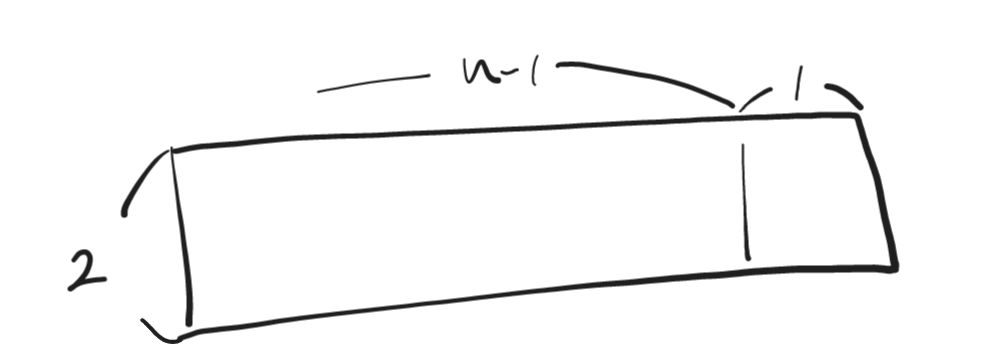
위의 그림에서 보듯이 가로 길이 n-1이 타일을 세워서 놓는 경우의 수 n으로 확장할 수 있는 경우는 많지 않습니다.

아래는 가로 길이 n-2에서 n까지 늘릴 수 있는 경우의 수입니다.

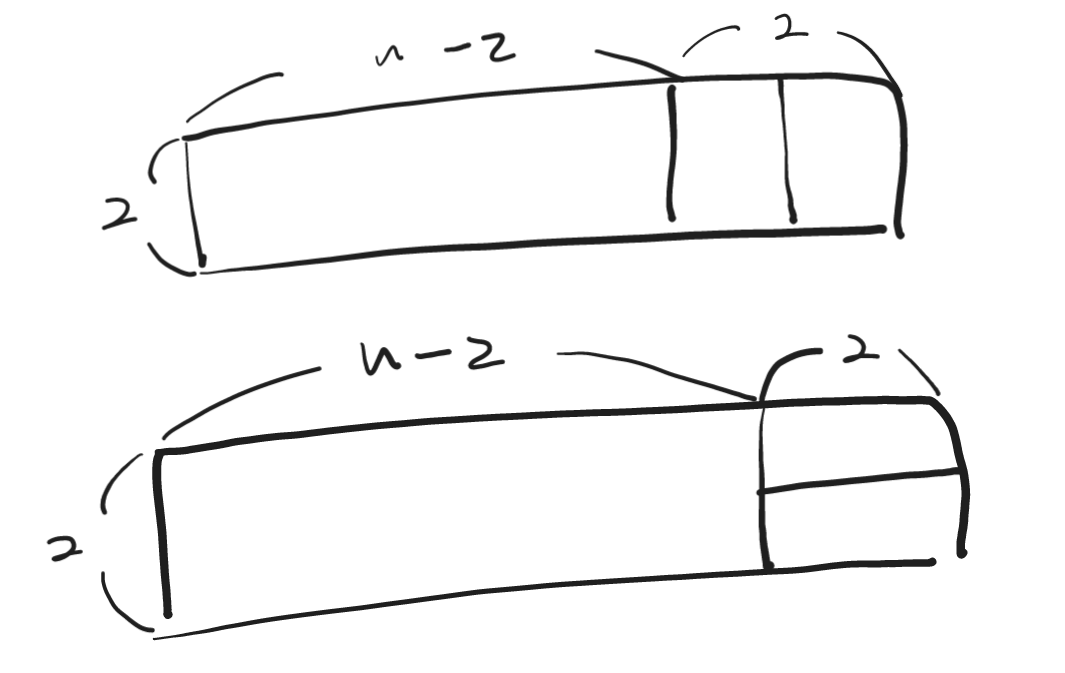
먼저 (그림 2)에서 상단 이미지를 보면(세로로 2개 붙였을 때), 가로 길이가 n-1에서 n으로 확장되었을 때와 같은 패턴을 보인다.
블록은 수직으로 장착됩니다.
따라서 위의 경우는 폭이 n-1인 경우의 수와 같습니다.

(∵ 그림 1에서 확장된 경우는 1개만 있음)

마지막으로 (그림 2)에서 가로 길이를 n-2에서 n으로 확장할 수 있는 경우의 수는 다음과 같다는 것을 알 수 있다.

가로 길이 n = 만들 수 있는 경우의 수 가로 길이 n-1을 만들 수 있는 경우의 수 + 가로 길이 n-2를 만들 수 있는 경우의 수 (세로이중확대, ‘||’형태) (가로이중확대, ‘=’형태)

따라서 문제의 재귀 방정식은 피보나치 수열의 재귀 방정식을 가집니다.
그러나 F(1) = 1이고 F(2) = 2입니다.

2 x 1 타일을 만들 수 있는 방법의 수는 ‘ | ‘ 하나의 틀로 2 x 2 타일을 만들 수 있는 방법의 수는

‘ = ‘, ‘ || ‘ 두 가지 형태가 있기 때문입니다.

코드를 풀다

알고리즘 문제를 풀 때 데이터 구조에 익숙해지기 위해 시간복잡도와 공간복잡도가 만족될 때 리스트 형식을 선호한다.
해결책은 다음과 같습니다.

N = int(input())
dp = (0 for _ in range(N))
dp(1:2) = (1,2)

def pibo(dp, N) :
    if 2 >= N :
        return dp(N)
    else :
        if dp(N) == 0 :
            dp(N) = pibo(dp,N-1) + pibo(dp, N-2)
        return dp(N)

print(pibo(dp, N) % 10007)

‘dp’ 목록은 피보나치 수열을 정의하는 목록입니다.

피보나치 수열의 인덱스를 ‘N’으로 정의하고 N이 3 이상이고 수열 요소의 초기화 값(0)에서 변화가 없을 때 재귀함수를 이용하여 피보나치 수열을 구성한다.

(* 초기화값과 관련된 조건이 없으면 초기화값 0을 시퀀스 값으로 인식하여 (1,2,3,0,0,0…)으로 출력합니다.
)

나는 그것을 느꼈다

다른 부분은 강하지 않은데 재귀함수 부분이 특히 어려워서 연습이 많이 필요한 것 같았어요. 반복되는 호출을 통해 파헤치는 방식이라 간단한 함수를 작성하는 것조차 여전히 매우 혼란스럽습니다.
이것은 DFS 문제 때문에 많은 부담을 느끼지만, 그것을 반복해서 풀면서 익숙해져야 합니다.