1. 1차원 및 2차원 특징 공간
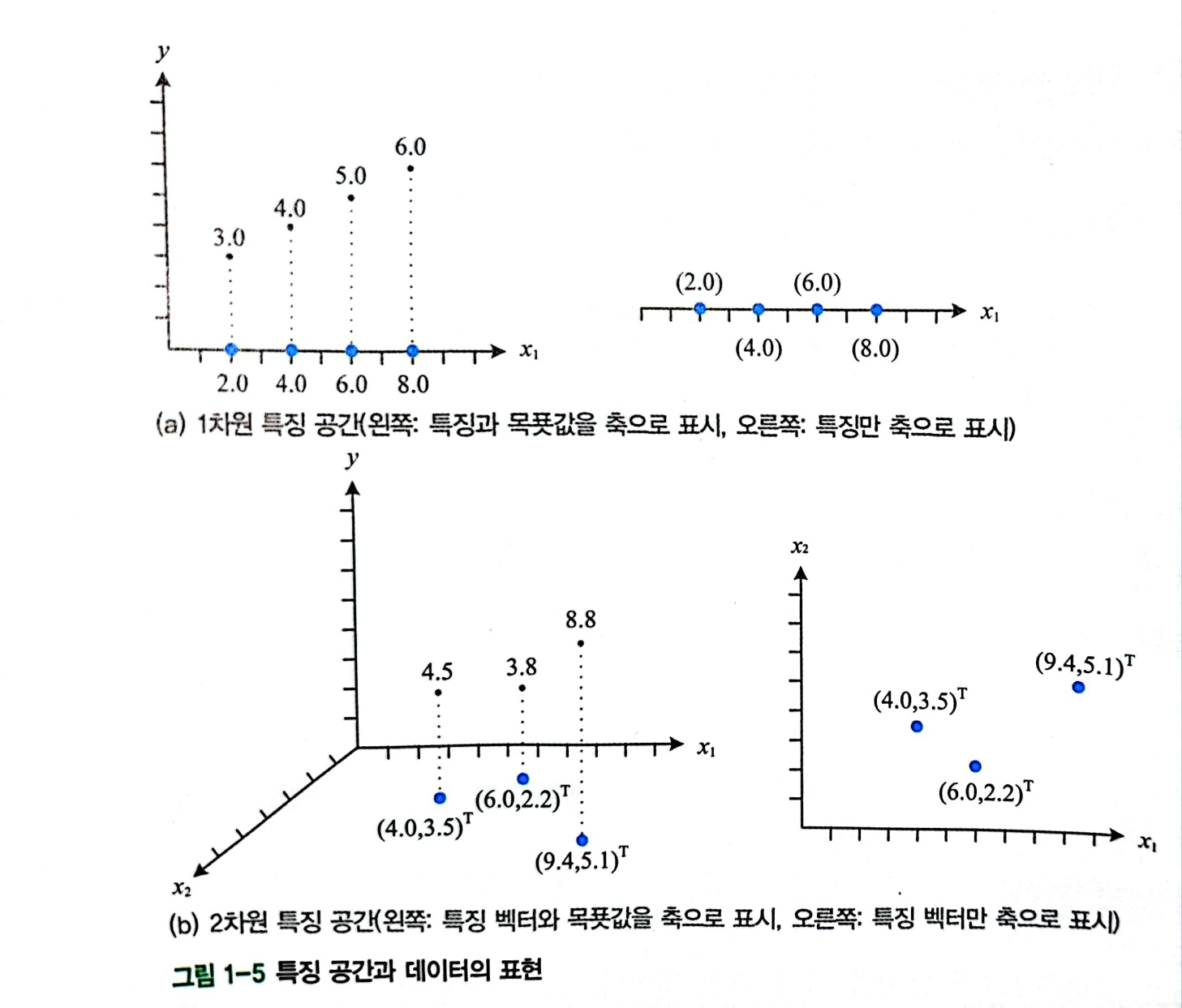
(그림 1-5(b))는 x1과 x2로 나누어 괄호 안에 (x1, x2)^T로 표현되는 두 개의 특성이 있는 상황입니다.
이제 특정 공간은 2차원이며 벡터 x = (x1,x2)^T로 표현됩니다. 왼쪽 그림에서는 세로축을 목표값으로 지정하여 높이로 표현하였고, 오른쪽 그림에서는 세로축을 2개의 피처에만 지정하였습니다.
2. 다차원 특징 공간
d차원 데이터를 식으로 표현하면, 엑스 = (x1, x2, …., xd)^T. 차원이 증가하면 모델의 매개변수 수도 증가합니다. 예를 들어 매개변수가 두 개인 직선이라는 모델을 한 차원에서 y=wx+b로 표현한다면 다음과 같이 d 차원에서 d+1 매개변수로 표현한다.
y = w1x1 + w2x2 + w3x3 + … + wdxd + b
2차 곡선을 모델로 선택하면 매개변수의 수가 더 늘어납니다.
1차원 특징 공간에 대한 2차 곡선의 방정식
y = w1x1^2 + w2x1 + b
d차원 특징 공간에 대한 2차 곡선의 방정식
y = w1x1^2 + w2x2^2 + … + wdxd^2 + wd+1x1x2+ … + wd^2xd-1xd + wd^2+1×1 + …. + wd^2+dxd + b
매개변수의 수는 3 또는 d^2+d+1입니다. 차원이 커질수록 모델의 차수가 높아질수록 추정해야 할 매개변수의 수도 많아져 더 어려운 문제가 된다.
3. 특징 공간 변환 및 표현 학습
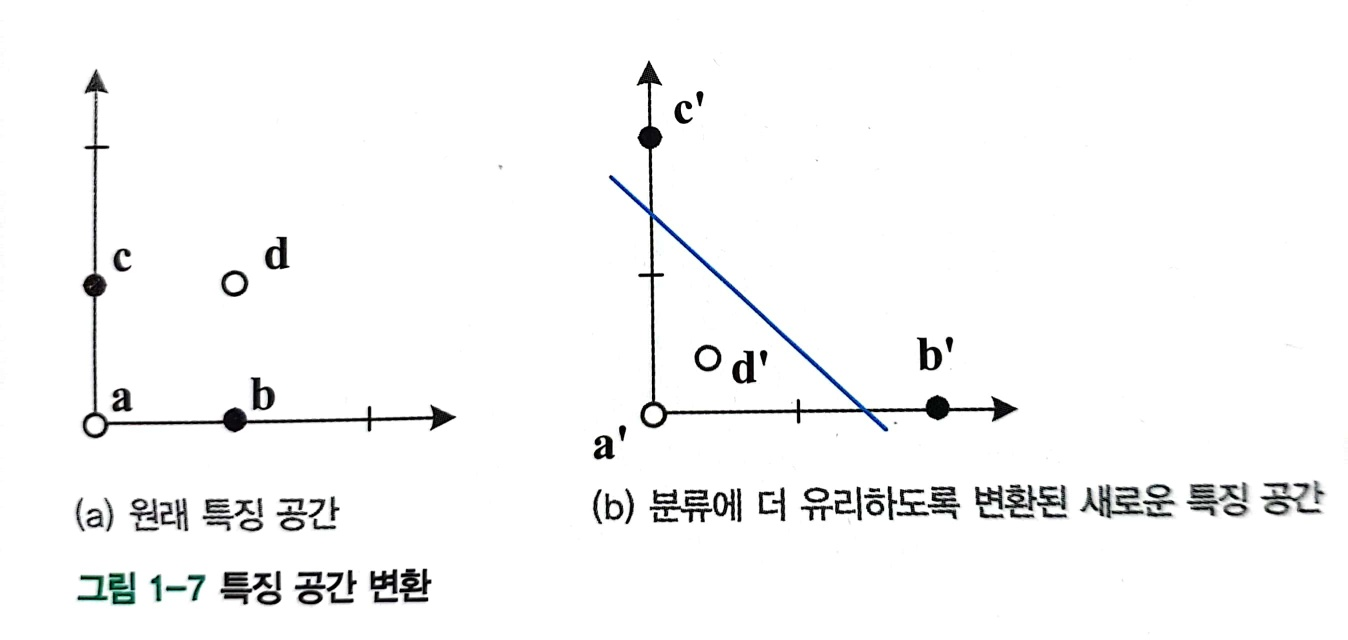
(그림 1-7(a))는 2차원 특징 공간에 분포된 4개의 샘플을 보여줍니다. 이것을 두 가지 범주로 분류하는 문제로 생각하면, ㅏ그리고 디카테고리에 속합니다 비그리고 씨그것이 나머지 클래스에 속한다고 가정합니다. 이 기능 공간은 다음 방정식을 사용하여 변환됩니다.

변환 후 4개 샘플 ABCD’새로운 분포에서 선형 모델을 사용하여 100% 정확도로 분류할 수 있는 다음과 같은 새로운 특징 벡터가 있습니다. 예를 들어, (그림 1-7)의 파란색 선은 4개의 샘플을 완벽하게 분류합니다.
a = (0, 0)^T → ㅏ’ = (0, 0)^T
b = (1, 0)^T → 비’ = (2, 0)^T
c = (0, 1)^T → 씨’ = (0, 2)^T
d = (1, 1)^T → 디’ = (0.4, 0.4)^T
차원이 증가한다고 해서 공식이나 알고리즘이 변경되어야 한다는 의미는 아닙니다.
예를 들어, 두 점 사이의 거리를 계산할 때 3차원 특징 공간에서 두 점 a = (a1, a2, a3)^T 및 b = (b1, b2, b3)^T가 주어지면 다음과 같이 생각할 수 있습니다. 계산대로
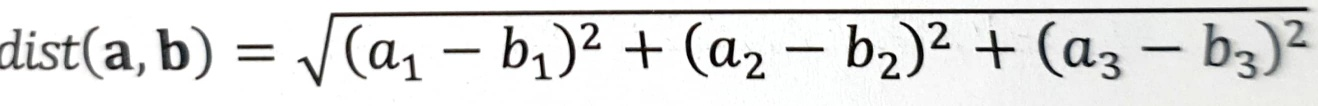
이 계산 방법을 d차원으로 확장하면 다음과 같은 식이 됩니다.
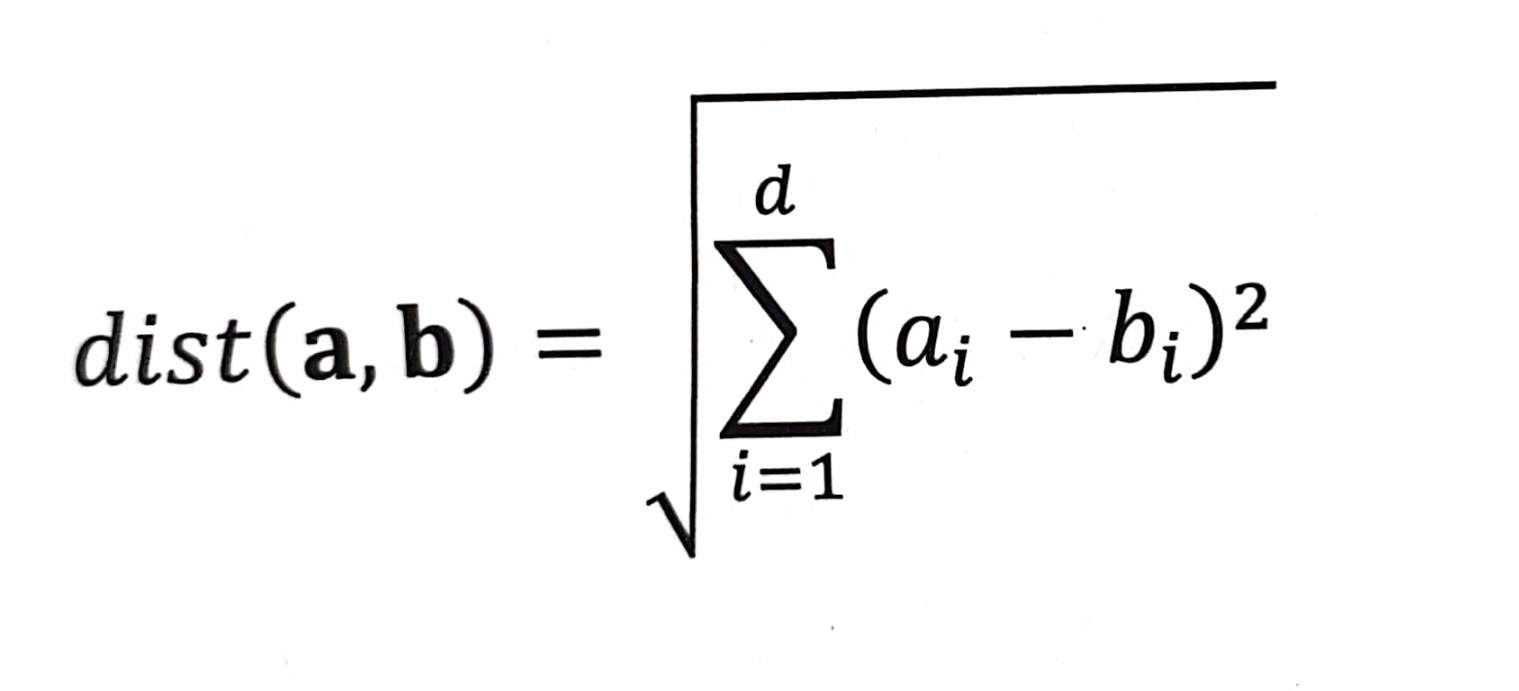
이 표현은 d의 모든 값에 적용되는 일반적인 표현입니다. 이와 같이 머신러닝에서는 저차원에서 개발한 방정식이나 알고리즘을 고차원에 그대로 적용할 수 있다. 그러나 차원이 커질수록 거대한 특정 공간이 형성되고, 그것이 야기하는 현실적 문제는 차원의 저주그것은 말한다.
